摘要:
北斗坐标系是北斗卫星导航系统的大地基准。本文在扼要叙述背景情况之后,首先给出了北斗坐标系原点、尺度、定向的定义和参考椭球的定义和导出常数;其次介绍北斗坐标系的首次实现,这次实现由北斗系统的8个监测站在历元2010.0的ITRF2014框架下的坐标和速度体现,它们是通过处理一个包括8个监测站的全球GNSS网4期GPS数据、框架对准与监测站坐标序列的线性回归拟合得到的;最后就参考框架的更新周期、监测站境外布设和连续观测、精密星历的生成与发布,北斗坐标系的标准化问题进行了讨论,并提出一些建议。
关键词:北斗坐标系;北斗卫星导航系统;参考框架;监测站
一个全球卫星导航定位系统的基本任务是为全球用户提供可用性、完好性、连续性和精度符合规定要求的导航定位服务。卫星导航系统赖以导航定位的大地基准是其使用的坐标系。坐标系对导航定位系统的重要性不言而喻。坐标系在很大程度上决定了导航系统的性能,特别是导航定位的精度。另外,坐标系也是决定一个导航系统的国际兼容性和系统互操作性的重要因素。
毫无疑问,一个全球卫星导航系统的大地基准应是一个地心的全球坐标系。根据2013年12月发布的北斗卫星导航系统空间信号接口控制文件,北斗导航系统的大地基准采用2000中国大地坐标系(CGCS2000)[1]。CGCS2000是我国的国家大地坐标系,2008年开始正式实施。在北斗系统建设的早期阶段,笔者利用2007—2009年的监测站GPS观测数据,计算了监测站的坐标和速度,建立了北斗系统的试用坐标系。实际上,这一试用坐标系,在严格意义上并不是CGCS2000,实际上更接近ITRF2000[2-3]。这一试用坐标系,在北斗系统的前期建设中曾经发挥了积极作用。但是,随着时间的推移,我们发现,将北斗系统的大地基准与国家大地坐标系捆绑一起是不适当的,不切实际的,对北斗系统的长远发展也是不利的。从长远观点来看,一个卫星导航系统,应该采用属于自己的独立大地基准[2]。GPS、GLONASS及Galileo均是如此[4-5]。北斗导航系统采用独立于国家大地坐标系,采用自己的专用坐标系,当属正确决策。于是,就提出了“北斗坐标系”。2017年12月,中国卫星导航系统管理办公室发布的《北斗卫星导航系统空间信号接口控制文件公开服务信号B2a(1.0版)》正式规定,北斗导航系统采用专用坐标系——北斗坐标系[6]。
本文简要介绍北斗坐标系的定义和首次实现,以及坐标精度评估,并就某些问题提出一些建议。
北斗坐标系是北斗卫星导航系统的大地基准。英文名称是BeiDou coordinate system,缩写BDCS。
北斗坐标系通过参考历元的地面监测站坐标和速度实现,称为参考架。
北斗坐标系将通过重新实现使参考框架最现时化和精度最佳化。坐标系的每次实现,对应产生一个新的参考框架。
随着时间的推移,北斗坐标系将出现多个参考架。不同参考架的标识是BDCS(W×××),括号内符号W×××标示该参考架开始执行的北斗系统时(BDT)第×××周的0秒。例如,BDCS(W465)、BDCS(W1002)分别标示从BDT时第465周0秒开始执行的参考框架和从BDT时第1002周0秒开始执行的参考框架。
北斗坐标系的原点、尺度与定向的定义如下。
原点:包括海洋和大气的整个地球的质量中心。
尺度:长度单位是m(SI)。这一尺度同地心局部框架的TCG时间坐标一致。
定向:在1984.0时初始定向与BIH的定向一致。
定向时间演变:定向随时间的演变使得整个地球的水平构造运动无整体旋转。
上述定义与IERS规范[7]一致。
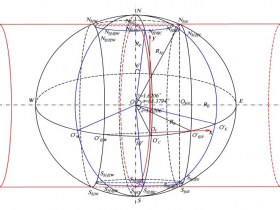
北斗坐标系为一右手直角坐标系。原点为地球质量中心,Z轴指向IERS参考极方向,X轴为IERS参考子午面与通过原点且同Z轴正交的赤道面的交线,Y轴完成右手直角坐标系,如图 1。
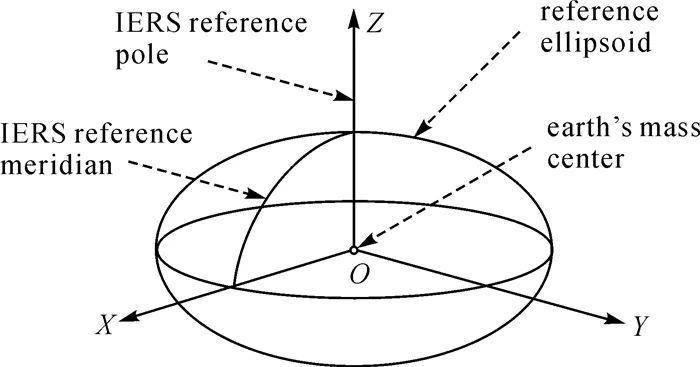
图1 BDCS参考椭球
北斗坐标系采用CGCS2000参考椭球,即CGCS2000坐标系的参考椭球,该参考椭球的定义常数和导出常数见表 1—表 3。
|
常数 |
数值 |
|
长半轴/m |
a=6 378 137.0 |
|
扁率 |
f=1:298.257 222 101 |
|
地心引力常数(包括大气层)/m3s-2 |
GM=3 986 004.418×108 |
|
地球自转角速度/rad s-1 |
ω=7 292 115.0×10-11 |
表1 BDCS参考椭球的定义常数
|
常数 |
数值 |
|
短半轴b/m |
6 356 752.314 1 |
|
线偏心率E/m |
521 854.009 700 25 |
|
极曲率半径c/m |
6 399 593.625 9 |
|
第一偏心率平方e2 |
0.006 694 380 022 90 |
|
第一偏心率e |
0.081 819 191 042 816 |
|
第二偏心率平方e′2 |
0.006 739 496 775 48 |
|
第二偏心率e′ |
0.082 094 438 151 917 |
|
轴比b/a |
0.996 647 189 319 |
|
子午圈一象限弧长Q/m |
10 001 965.729 3 |
|
椭球体积V/km3 |
1 083 207 319 783.546 |
|
椭球表面积S/km2 |
510 065 621.718 |
|
平均半径R1/m |
6 371 008.771 4 |
|
同面积之球的半径R2/m |
6 371 007.180 9 |
|
同体积之球的半径R3/m |
6 371 000.790 0 |
表2 BDCS参考椭球的导出几何常数值
|
常数 |
数值 |
|
椭球面正常位U0/m2s-2 |
62 636 851.714 9 |
|
2阶带谐系数J2 |
0.108 262 983 225 8×10-2 |
|
4阶带谐系数J4 |
-0.237 091 125 614 1×10-5 |
|
6阶带谐系数J6 |
0.608 346 525 889 2×10-8 |
|
8阶带谐系数J8 |
-0.142 681 100 979 8×10-10 |
|
10阶带谐系数J10 |
0.121 439 338 334 3×10-13 |
|
赤道正常重力γe/ms-2 |
9.780 325 336 1 |
|
极正常重力γp/ms-2 |
9.832 184 937 9 |
|
平均正常重力γ/ms-2 |
9.797 643 222 4 |
|
m=ω2a2b/(GM) |
0.003 449 786 506 78 |
|
k=bγp/aγe-1 |
0.001 931 852 619 31 |
|
地球质量M(包括大气)/kg |
5.973 331 96×1024 |
表3 BDCS参考椭球的导出物理常数值
CGCS2000参考椭球的几何中心与坐标系的原点重合,旋转轴与坐标系的Z轴一致。
CGCS2000参考椭球为一等位旋转椭球,参考椭球面既是大地经纬度、高程的几何参考面,又是地球外部正常重力场的参考面。
北斗坐标系通过地面监测站在参考历元的坐标和速度实现。因此如何获得监测站的坐标和速度,以及如何进行框架对准是北斗坐标系实现的关键。在本次实现中,监测站的坐标通过GNSS数据处理得到,参考框架对准通过最小约束法实现。
因早期北斗系统不具备全球观测能力,为了实现并维持其坐标系,截至2016年,在北斗系统地面监测站进行了4期GPS观测。第1期为2007—2009年,各站观测依次单独进行。第2期从2011年12月16日至12月31日,连续观测15 d,8个监测站同步联测。第3期从2014年4月24日至5月8日,连续观测15 d,8个监测站同步联测。第4期于2016年5月至11月单独观测完成。
实现北斗坐标系的数据处理分3个步骤。第1步是联合处理由全球IGS站、国内陆态网基准站和北斗地面监测站组成的全球GNSS网数据得到监测站坐标的单日松弛解;第2步采用最小约束法将北斗监测站坐标单日解体现的框架,对准ITRF2014框架;第3步是将经框架对准的监测站坐标序列进行线性回归拟合,得到历元2010.0的监测站坐标和速度,最终实现北斗坐标系。
2.1 站坐标松弛解
在全球选取均匀分布且稳定可靠的62个IGS站,国内选取27个陆态网基准站,与8个北斗地面监测站组成全球GNSS网。全球网GPS数据处理用GAMIT10.5软件。软件采用绝对天线相位中心模型、FES2004海潮模型。为了更好地保持网形结构同时不影响松弛解解算结果,国际IGS站坐标给予1 m约束,国内基准站坐标给予10 m约束。除其他参数,输出参数包括站坐标单日松弛解及其协方差矩阵。
2.2 框架对准
监测站坐标单日松弛解是有先验松约束的站坐标解。在框架对准之前,需要将先验松约束去除。为此,执行去约束运算[8-11]
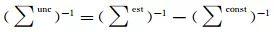 (1)
(1)
式中,∑unc代表去约束后的坐标协方差阵;∑est代表坐标松弛解的协方差阵;∑const代表加入的先验约束值。
然后,采用如下方程加入最小约束[10-12],将去约束解体现的框架对准于由62个IGS站ITRF2014(http://itrf.ensg.ign.fr/ITRF_solutions/2014/ITRF2014.php)坐标定义的参考基准
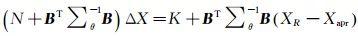 (2)
(2)
式中,N=(∑unc)-1;ΔX=XC-Xapr, Xapr是站坐标近似值(松弛解采用的概略坐标),XC是松弛解的站坐标;K是松弛解法方程自由项;B=(ATA)-1AT,A是由概略坐标构成的偏导数设计矩阵
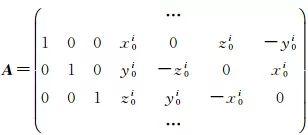 (3)
(3)
根据式(2),得到北斗监测站4期观测时段的ITRF2014坐标序列。
2.3 参考历元坐标和速度计算
用线性回归方程拟合监测站4期站坐标序列,未知参数取坐标和速度,协方差矩阵由坐标时间序列的方差确定,从而得到历元2010.0的监测站ITRF2014框架下的坐标和速度。表 4列出得到的监测站速度及其标准差。此外,为了验证结果的可靠性,将此次计算结果与前3期观测数据的计算结果进行比较,发现北斗监测站坐标差异不到1 mm。
|
m/a |
||||||
|
站名 |
VX |
VY |
VZ |
σVX |
σVY |
σVZ |
|
北京 |
-0.010 93 |
-0.040 10 |
-0.038 60 |
0.000 7 |
0.000 5 |
0.000 5 |
|
成都 |
-0.033 07 |
-0.003 87 |
-0.007 63 |
0.000 2 |
0.000 2 |
0.000 3 |
|
哈尔滨 |
-0.029 93 |
-0.007 43 |
-0.007 63 |
0.000 4 |
0.000 4 |
0.000 4 |
|
喀什 |
-0.032 20 |
-0.004 53 |
0.011 57 |
0.000 3 |
0.000 2 |
0.000 2 |
|
汕头 |
-0.032 77 |
-0.007 53 |
-0.010 33 |
0.000 3 |
0.000 2 |
0.000 4 |
|
三亚 |
-0.030 37 |
-0.001 43 |
-0.009 07 |
0.000 5 |
0.000 3 |
0.000 6 |
|
乌鲁木齐 |
-0.031 73 |
0.000 17 |
0.004 63 |
0.000 3 |
0.000 3 |
0.000 3 |
|
拉萨 |
-0.046 00 |
-0.008 60 |
0.012 10 |
0.000 2 |
0.000 1 |
0.000 2 |
表 4 北斗监测站速度及标准差
(1) 关于坐标系重新实现周期。一个坐标系的每次实现无论多么精确,随着时间的推移,监测站坐标和速度的误差积累将越来越大,以致坐标系重新实现成为不可避免。坐标系重新实现的结果就是框架的更新。重新实现就是利用历时更长的观测数据重新确定监测站坐标,并将框架对准于最新的ITRF框架。现在的问题是,参考框架更新周期多长比较合适?一般而论,总的原则是,以北斗框架与ITRF框架的失准度小于规定的限差为准,或者简单的,北斗框架更新与ITRF框架更新的周期相同,更新时间可以稍有落后。当然,也可以根据其他实际情况而定,例如由于监测站的数量变动或升级改造,框架需要更新。笔者建议,一般情况下,北斗框架的更新周期可以采用ITRF的更新周期但稍有滞后。
(2) 关于监测站境外布设与连续观测。鉴于北斗系统的全球性质,监测站的境外扩展是必要的,也是必然的,这无疑有利于改善坐标系的实现精度。另外,假若监测站采用长期连续观测,对改善框架精度和现势性同样有益处。如果拥有长期连续观测数据,数据处理方法当然需要相应改变,或许可以采用监测站运动非线性假设,有可能得到更逼真的监测站速度。因此,笔者建议,监测站的境外布设以及长期连续观测,应是今后努力方向之一。
(3) 关于卫星精密星历。如前所述导航系统的坐标系通过参考历元的监测站坐标和速度实现。这是实现坐标系的最基本形式,因为监测站坐标是卫星轨道确定必不可少的输入参数。作为卫星定轨的输出,卫星星历也是坐标系的重要体现(或实现)。卫星星历分为精密星历和广播星历。精密星历的精度为厘米级,即代表厘米级精度的参考框架。广播星历实际上是精密轨道的外推,精度一般在米级水平,甚至更低一些,代表低精度的参考框架。广播星历是用户最容易得到的坐标系产品。精密星历甚至也可以从网站下载得到。为了北斗系统应用的推广,对于精密定位(点定位和相对定位),有必要组织例行化的北斗卫星精密星历的生成,并通过有效形式向用户发布。
(4) 关于北斗坐标系的标准化。卫星星历(轨道)既然是重要的坐标系产品,那么卫星定轨所用的卫星动力学模型、地球重力场模型、天球参考系与地球参考系之间的转换模型和地球定向参数,以及其他一些重要常数,当属坐标系的重要内容。在实际工作中,应将这些元素纳入坐标系一起考虑。为了使坐标系产品生产的规范化,与北斗坐标系工作的正规化,建议在条件成熟时,有必要制定北斗坐标系标准,以便实际工作有所遵循。
(1) 北斗系统采用专用的地心大地基准。
(2) 北斗系统的大地基准中文名称是北斗坐标系,英文名称是BeiDou coordinate system,英文缩写BDCS。
(3) 北斗坐标系的不同框架的标识是“BDCS(W×××)”,其中W×××标示该框架自北斗系统时第×××周0秒开始执行。
(4) 北斗坐标系的原点、尺度、定向与IERS规范规定一致,参考椭球采用CGCS2000椭球。
(5) 北斗坐标系通过监测站坐标和速度与卫星星历实现。北斗坐标系还包括参考椭球、重力场模型、地球定向参数以及坐标转换参数等。
(6) 北斗坐标系的首次实现,包括参考历元2010.0时8个监测站ITRF2014框架下坐标和速度,通过8个监测站4期GNSS数据与62个国际IGS站和27个国内陆态网络基准站数据的联合解算得到监测站坐标松弛解、框架对准与监测站坐标序列线性回归拟合得到。坐标标准差小于2 mm,速度标准差小于1 mm/a。
关于北斗坐标系工作,提出如下建议:
(1) 北斗坐标系的重新实现周期一般与ITRF相同。
(2) 北斗系统采取全球跟踪与连续观测。
(3) 组织北斗卫星精密星历的生成与发布。
(4) 注意北斗坐标系的标准化工作。
文章转自网络